domingo, 15 de maio de 2016 versão para imprimir - aqui O primeiro Ás preto adaptado de Rodas, Vida e Outras Diversões Matemáticas, Martin Gardner Baralham-se 52 cartas e colocam-se em cima da mesa, voltadas para baixo. Depois vão-se tirando as cartas, uma por uma, com a face voltada para cima, começando pelo cimo do baralho. Se pedissem ao leitor para apostar em quantas cartas era preciso tirar até aparecer o primeiro ás preto, que posição (1ª, 2ª, 3ª, …) escolheria de modo que, se o jogo fosse repetido muitas vezes, otimizasse a sua possibilidade de acertar? solução resolução domingo, 01 de maio de 2016 versão para imprimir - aqui Números repetidos de Olimpiadas Populares y concursos nacionales 05-06 (Cuba) Quantos números entre 1 e 2006 se podem escrever utilizando exatamente dois dígitos diferentes? Por exemplo, 1919 cumpre a condição e 1231 não cumpre. solução resolução sexta feira, 15 de abril de 2016 versão para imprimir - aqui Leite fresquinho! de VI OPM Quatro vacas pretas e três vacas castanhas dão em cinco dias tanto leite como três vacas pretas e cinco vacas castanhas em quatro dias. Qual o tipo de vaca que dá mais leite? solução resolução sexta feira, 01 de abril de 2016 versão para imprimir - aqui Quatro amigos no Arranha-céus de Desafios, José Paulo Viana O Pedro, o Zé, o António e o Miguel moram em diferentes andares de um prédio bastante alto. O Miguel vive seis andares acima do Zé. O António, para ir de elevador até casa do Miguel, demora o dobro do que para ir até ao andar do Zé. Com o Pedro acontece o mesmo: a viagem de sua casa até à do Miguel dura o dobro do que se fosse até ao andar do Zé. Quando o Pedro quer visitar o António, como tem de descer, vai sempre pelas escadas. Quantos andares desce ele? solução resolução terça feira, 15 de março de 2016 versão para imprimir - aqui Canteiro triangular de XXIV OPM, Categoria A O quintal do Sr. 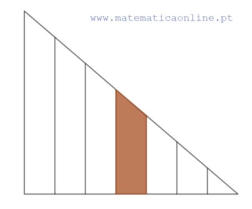Joaquim tem a forma de um triângulo retângulo e está dividido em sete canteiros de igual largura, como se indica na figura. A área do quintal é 21 m 2 . Qual é a área do canteiro sombreado? solução resolução terça feira, 01 de março de 2016 versão para imprimir - aqui Números e restos Qual é o menor número em que penso quando o resto da divisão por 2, 3, 4, 5 e 6 dá um número diferente de zero e todos os restos são diferentes entre si? 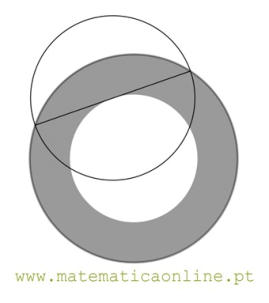solução resolução segunda feira, 15 de fevereiro de 2016 versão para imprimir - aqui A fantástica pista de corridas adaptado de Fascínios da Matemática, a descoberta da matemática que nos rodeia, Theoni Pappas Consideremos uma pista de corridas circular, de qualquer tamanho, formada por dois círculos concêntricos (exemplificado na figura). Qual a relação entre a área da pista e a área do círculo cujo diâmetro é a corda do círculo maior tangente ao círculo menor? solução resolução segunda feira, 01 de fevereiro de 2016 versão para imprimir - aqui Trabalhos forçados No dia em que os pais do Francisco fazem anos de casados é costume ficarem num hotel, deixando os filhos em casa com uma listagem de tarefas para cumprirem. A parte problemática da questão é que o Francisco e as duas irmãs não se entendem quanto à divisão dessas tarefas. – Eu posso ir ver a caixa do correio! – prontificou-se o Francisco. – Nem penses! E estás à espera que em troca eu faça o almoço… - ironizou a Beatriz. – Eu posso regar o jardim, mas vocês aspiram a casa… – sugeriu a Joana. Mas as intervenções deste tipo só serviam para aumentar a confusão: porque regar o jardim era mais fácil do que…, porque lavar o carro era pior do que… Ninguém se entendia. – Calma! – sugeriu o Francisco. – Já vimos que assim não chegamos a lado nenhum! Temos 10 tarefas, de 1) a 10), para distribuir entre nós e essas tarefas não têm o mesmo grau de dificuldade, portanto, é impossível chegar a um consenso. E que tal tentar reparti-las de modo que nenhum de nós se sinta prejudicado?... – Isso era o ideal! – concordou a Beatriz. – Mas é isso que estamos a tentar fazer… – Não é bem assim! Diz antes que cada um de nós está a tentar escolher as tarefas mais fáceis! Estou a pensar num processo que permita dividir as tarefas de modo que nenhum de nós possa queixar-se… – Mas isso é impossível. Ainda não dividimos nenhuma e já todos nos queixamos – observou a Joana. – O melhor é sortear as tarefas, como fazemos todos os anos… – Nem pensar! – explodiu a Beatriz. – Com o azar que habitualmente tenho, fico com todas as tarefas difíceis. Mais vale cada um escolher uma tarefa até esgotar as tarefas. – Eu não quero ser a primeira a escolher! – anunciou a Joana, perspicaz. Rapidamente todos perceberam que a Joana tinha razão. O primeiro a escolher seria o mais prejudicado. Voltava tudo à estaca zero. – Pois eu penso que é possível dividir as tarefas de modo que nenhum de nós possa contestar a divisão de tarefas que for feita. E não estou a falar de sorteio… A Joana e a Beatriz olharam-se surpreendidas. Valia a pena ouvir o que o Francisco tinha para dizer. solução resolução sexta feira, 15 de janeiro de 2016 versão para imprimir - aqui Pulseira de pérolas – Francisco… Francisco, arranja-me a pulseira. – E a irmã entregou-lhe um fio e 10 esferas a imitar pérolas. Eram 8 brancas e 2 pretas, cada uma com um pequeno furo para passar o fio. – És incrível! Rebentas o fio todos os dias… – Prometo que não volta a acontecer. É só mais esta vez. – O Francisco começou a enfiar as pérolas no fio, mas ao contrário de outras vezes, a irmã mostrou-se bastante exigente. – Não! Assim não… começa com a pérola preta! Não!... Coloca antes as duas pérolas pretas no meio. Não… – Pára! Tens de te decidir. É que existem imensas possibilidades para combinar todas as pérolas e por este andar nunca mais sairemos daqui. A irmã decidiu-se por uma combinação, mas o Francisco ficou a pensar de quantas formas poderia colocar as pérolas de modo a obter pulseiras com aspetos diferentes. Quantas serão essas possibilidades? solução resolução sexta feira, 01 de janeiro de 2016 versão para imprimir - aqui Farol à vista de Ginástica Mental, Treino para o cérebro Desenhe em algumas células um barco, de forma a que este não toque nenhum outro barco ou farol, nem sequer na diagonal. Os algarismos dos faróis indicam quantos barcos se podem ver dele na horizontal ou na vertical. Não importa se entre um barco e um farol se encontra outro barco ou farol. Todos os barcos se veem, pelo menos, de um farol. solução resolução