Site de divulgação matemática - Aulas Online - Explicações - Vídeos

Algoritmo da raiz quadrada
versão para imprimir - aqui
Existem várias formas de nos aproximarmos do valor da raiz
quadrada de um número. Uma delas, a equação de Pell,
permite encontrar a parte inteira para de uma raiz quadrada de
uma forma simples e rápida, apenas recorrendo à subtração de
números inteiros ímpares e contando o número de operações
efetuadas.
Exemplo 1
Qual a parte inteira da raiz quadrada de 32.
1º.
32 – 1 = 31
2º.
31 – 3 = 28
3º.
28 – 5 = 23
4º.
23 – 7 = 16
5º.
16 – 9 = 7
Não se dá continuidade ao processo, uma vez que na próxima subtração o valor que se irá obter é negativo.
Como foram feitas 5 subtrações, a parte inteira da raiz de 32 é 5.
Exemplo 2
Qual a parte inteira da raiz quadrada de 36?
1º.
36 – 1 = 35
2º.
35 – 3 = 32
3º.
32 – 5 = 27
4º.
27 – 7 = 20
5º.
20 – 9 = 11
6º.
11 – 11 = 0
O número de subtrações feitas foi 6, assim a parte inteira de raiz quadrada é 6 e como na última subtração o
resultado foi zero, significa que 36 é um quadrado perfeito e a sua raiz é o valor 6.
Este método acaba por nos dar o valor da raiz quadrada quando se trata de quadrados perfeitos, caso contrário
apenas ficamos a saber o valor da parte inteira da raiz quadrada de um número. Contudo, existem outros
métodos que nos permitem obter melhores aproximações, como é o caso do próximo algoritmo. Algoritmo que
permite calcular a raiz quadrada de qualquer número e com a aproximação desejada.
Vamos analisar o método através de alguns exemplos.
Exemplo 3
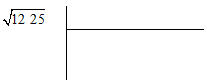
Como calcular o valor da raiz quadrada de 1225, isto é,
.
1.
Começamos por dividir o número 1225, da direita para a esquerda, em classes de 2 algarismos.
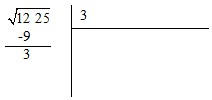
2.
Calculamos mentalmente o número, cujo quadrado seja o valor mais próximo da classe da esquerda,
mas nunca superior. No exemplo é o número 3, pois 3
2
= 9, mas 4
2
já é superior a 12, colocamos esse
número no espaço à direita.
3.
Coloca-se o quadrado do número que encontrámos debaixo da classe da esquerda e fazemos a subtração.
4.
À direita da diferença escreve-se o seguinte grupo de algarismos (25) e debaixo de 3 escreve-se o seu
dobro.
5.
De 325, separa-se o algarismo da direita, 5, e divide-se o número à esquerda, 32, por 6, obtendo-se 5.
Coloca-se este valor à direita de 6 e multiplica-se o número obtido pelo mesmo valor do quociente, o 5.
6.
O produto obtido tem de ser menor ou igual ao número que se encontra à esquerda. Se for, efetua-se a
subtração do número da esquerda pelo produto e aceita-se o 5 como o segundo número da raiz quadrada.
Caso contrário temos de ir diminuindo o valor do quociente até encontrar um em que o produto seja
inferior.
Logo,
.
Exemplo 4
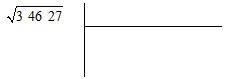
Determinar
com um erro inferior às centésimas.
1.
Começamos por dividir o número 34627, da direita para a esquerda, em classes de 2 algarismos.
2.
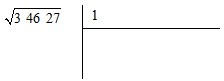
Calculamos mentalmente o número, cujo quadrado seja o valor mais próximo da classe da esquerda,
mas nunca superior. No exemplo é o número 1, pois 1
2
= 1, mas 2
2
= 4 já é superior a 3, colocamos esse
número no espaço à direita.
3.
Coloca-se o quadrado do número que encontrámos debaixo da classe da esquerda e fazemos a subtração.
4.
À direita da diferença escreve-se o seguinte grupo de algarismos (46) e debaixo de 1 escreve-se o seu
dobro.
5.
De 246, separa-se o algarismo da direita, 6, e divide-se o número à esquerda, 24, por 2, obtendo-se 12.
Como o número obtido é superior a 9, vamos começar por considerar o 9, colocando-o à direita de 2 e
multiplica-se o número obtido pelo mesmo valor considerado.
Como o produto obtido é superior a 246, vamos descartar o número 9 e experimentar um número inferior, o 8.
Dado que 224 é inferior a 246, aceita-se o 8 como segundo número da raiz quadrada e efetua-se a subtração do
número da esquerda pelo produto obtido.
6.
À direita da diferença escreve-se o próximo grupo de algarismos (27) e debaixo de 18 o seu dobro.
7.
Tentamos agora encontrar um número que ao colocar à direita de 36 e multiplicando por esse número
obtemos um produto igual ou inferior a 2227. Comecemos por experimentar o 7.
Não serve o 7, pois 2569 é superior a 2227, tentemos agora com o 6.
Este número já deverá ser aceite pois é inferior a 2227, aceita-se o 6 como terceiro número da raiz quadrada e
efetua-se a subtração do número da esquerda pelo produto obtido.
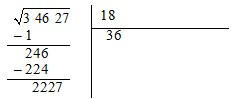
Desta forma, obtivemos a parte inteira da raiz quadrada que é 186, podemos continuar o processo para obter
uma melhor aproximação, para isso vamos acrescentado 00 como o próximo grupo de números, à direita de 186
colocamos uma vírgula e por baixo o seu dobro.
8.
Tentamos agora encontrar um número que ao colocar à direita de 372 e multiplicando por esse número
obtemos um produto igual ou inferior a 3100. Mas qualquer número que se coloque à direita de 372 fará
com que fique superior a 3100, então a única solução será o 0.
Adicionamos o 0 ao valor da raiz e acrescentamos mais um grupo de 00.
9.
Introduzimos o dobro de 1860 (não consideramos a vírgula) e voltamos a procurar um algarismo que ao
colocar à direita de 3720 e multiplicando por esse algarismo dê um número igual ou inferior a 310000.
Verificamos que não serve o algarismo 9, mas 8 é o algarismo procurado.
Acrescentamos 8 ao valor da raiz e subtraímos o produto ao número da esquerda.
Desta forma obtemos o valor aproximado da raiz quadrada com erro inferior às centésimas,
,
pode-se dar continuidade ao algoritmo até obter a aproximação desejada.
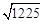
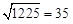
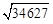
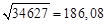


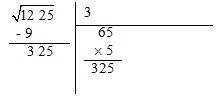
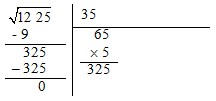

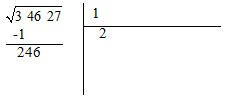
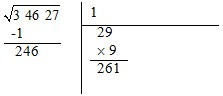
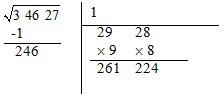
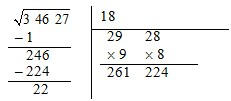
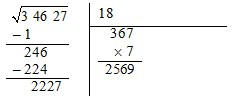
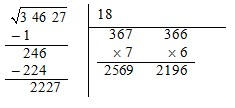
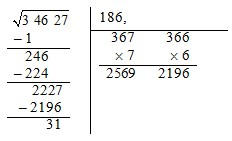














@2020 por Nuno Rosário
Contactos
965476488
geral@matematicaonline.pt


